Of the two core parameters of risk, likelihood is the least well understood within the infosec risk management community. So I feel it’s time to draw attention to some assumptions and issues that lead to error, and to suggest a way forward to improvement.
We can assess likelihood using either a frequentist or a probabilistic representation.
Frequentist assessment attempts to estimate the likelihood of an event occurring on the basis of the expected interval between events: once a month, once a year and so on. It’s currently the preferred approach in the infosec community, to the extent that it dominates the guidance provided by international standards and is widely considered to be ‘best practice’. This may be because it’s easy to visualise without any formal training, but unfortunately it suffers from some failings that make it untrustworthy.
It assumes that events occur with constant regularity. But although courtesy of the statistical Law of Large Numbers the intervals between very large numbers of randomly spaced events tend to a stable average, there’s no equivalent ‘Law of Small Numbers’. The average interval between small numbers of such events is generally a poor predictor of an individual event occurring. But even for large numbers of events, the average can be uninformative in a given case because the dispersion (the width of the range between the maximum and minimum event frequencies) can be very large, so the actual rate of occurrence at any particular moment may be far from the average. Failure to recognise this all too often underpins a tacit assumption that the clock starts when your project starts. But considering a ‘once in ten years’ event to be irrelevant if your project or service has a life of, say, a couple of years ignores the fact that the notional rate is only an average. The overlooked ‘once in ten years’ event could quite possibly occur twice next Tuesday.
Dangerous as these assumptions are, the frequentist representation of likelihood has an overriding intrinsic flaw – it prevents aggregation of risk factors.
Nothing happens without causes. Real risk events result from coincidence of typically multiple contributory factors, and the likelihood of an event obviously depends on the likelihoods of its contributory factors. These combine in strict mathematical ways depending on the logical relationships between the factors, but unfortunately the math doesn’t work if we use the frequentist representation. So frequentist assessment can’t be based on causality, but can only be plucked from past experience of the totalities of similar scenarios. This can be sufficient in fields such as motor insurance where causalities are relatively simple and unchanging, but the information security landscape is too complicated and too unstable to deliver adequate historical records. Consequently prediction on this basis will not yield results that accord with reality.
To get nearer the truth, we must rely on the mathematics of probability. But before you cringe in horror, only the basic principles are required, and they’re actually quite simple.
Probabilistic assessment represents the estimated likelihood of a single instance of an event occurring within some constant frame of reference – for our purposes usually a fixed time interval – on a scale of zero to one (or, equivalently, zero to 100 per cent). The fundamental advantage of this representation over the frequentist one is that it allows the use of valid math to aggregate risk factor likelihoods. So instead of having to guess a likelihood for an entire scenario, we can in principle calculate a scenario likelihood from the likelihoods of its contributory factors. The result is increased reliability through improvement in both the realism of individual assessments and the consistency with which multiple assessments can be performed.
In his snappily titled 1853 blockbuster An investigation of the laws of thought on which are founded the mathematical theories of logic and probabilities George Boole demonstrated that the fundamental mathematics of probability are essentially the same as the core mathematics of propositional logic – familiar to us as the Boolean algebra used by digital systems designers.
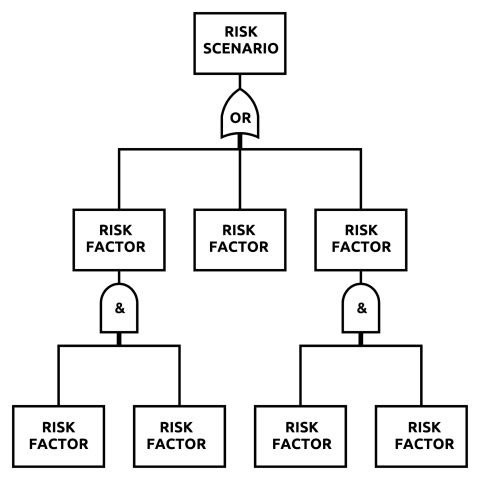 So how do we make effective use of the probabilistic representation of likelihood? Merely assigning notional probabilities to scenarios against a quantised scale won’t get us any further than using frequentist assessment. But investigating causalities can hugely improve the quality of results. The first step is to build a ‘factor tree’ from our risk scenario. This consists of successive tiers of causal factors connected at each level by their logical relationships. In each tier, several factors that must all occur to create an outcome are coupled by logical AND, whereas several alternative factors, any one of which is sufficient to cause the outcome are connected by logical OR. Replacing the logical relationships with the relevant probabilistic equations allows us to calculate the aggregate probability of the scenario cumulatively from the probabilities of its causal factors.
But where’s the gain? Provided the factor tree is sufficiently exhaustive – that is, crucially, that we’ve understood the scenario and its causes well enough – the method massively reduces the uncertainties that render the results of frequentist assessment questionable. Quite apart from the weaknesses already mentioned, when using a frequentist scale we are obliged to slot events into typically quite broad categories of likelihood before any risk calculations are performed. This causes actual event likelihoods that fall somewhere between the defined category boundaries (in practice, almost all event likelihoods) to be variably misrepresented, leading to significant but subsequently undetectable assessment error. The probabilistic factor tree allows a much closer approximation to reality as likelihood values are determined by the relationships between the factors in the tree rather than being distorted by forcing them into a limited number of arbitrarily pre-defined categories.
The bottom line is that reliable risk assessment absolutely depends on understanding and applying the core axioms of probability theory, as these are a formal expression of what actually happens. So to ignore probability theory is to ignore reality. The fundamentals first appeared in De Ratiociniis in Ludo Aleae, a pamphlet on the chances of winning at dice published by Dutch polymath and gambler Christiaan Huygens in 1657. Particularly as it’s not ‘scary math’, it’s utterly appalling that after three and a half centuries this elementary but crucial body of knowledge still doesn’t feature in mainstream risk management practitioner training. For now, learning it is a case of DIY but it’s essential. Otherwise we’ll just continue unwittingly generating random numbers while kidding ourselves we’re assessing risk.
So how do we make effective use of the probabilistic representation of likelihood? Merely assigning notional probabilities to scenarios against a quantised scale won’t get us any further than using frequentist assessment. But investigating causalities can hugely improve the quality of results. The first step is to build a ‘factor tree’ from our risk scenario. This consists of successive tiers of causal factors connected at each level by their logical relationships. In each tier, several factors that must all occur to create an outcome are coupled by logical AND, whereas several alternative factors, any one of which is sufficient to cause the outcome are connected by logical OR. Replacing the logical relationships with the relevant probabilistic equations allows us to calculate the aggregate probability of the scenario cumulatively from the probabilities of its causal factors.
But where’s the gain? Provided the factor tree is sufficiently exhaustive – that is, crucially, that we’ve understood the scenario and its causes well enough – the method massively reduces the uncertainties that render the results of frequentist assessment questionable. Quite apart from the weaknesses already mentioned, when using a frequentist scale we are obliged to slot events into typically quite broad categories of likelihood before any risk calculations are performed. This causes actual event likelihoods that fall somewhere between the defined category boundaries (in practice, almost all event likelihoods) to be variably misrepresented, leading to significant but subsequently undetectable assessment error. The probabilistic factor tree allows a much closer approximation to reality as likelihood values are determined by the relationships between the factors in the tree rather than being distorted by forcing them into a limited number of arbitrarily pre-defined categories.
The bottom line is that reliable risk assessment absolutely depends on understanding and applying the core axioms of probability theory, as these are a formal expression of what actually happens. So to ignore probability theory is to ignore reality. The fundamentals first appeared in De Ratiociniis in Ludo Aleae, a pamphlet on the chances of winning at dice published by Dutch polymath and gambler Christiaan Huygens in 1657. Particularly as it’s not ‘scary math’, it’s utterly appalling that after three and a half centuries this elementary but crucial body of knowledge still doesn’t feature in mainstream risk management practitioner training. For now, learning it is a case of DIY but it’s essential. Otherwise we’ll just continue unwittingly generating random numbers while kidding ourselves we’re assessing risk.
 So how do we make effective use of the probabilistic representation of likelihood? Merely assigning notional probabilities to scenarios against a quantised scale won’t get us any further than using frequentist assessment. But investigating causalities can hugely improve the quality of results. The first step is to build a ‘factor tree’ from our risk scenario. This consists of successive tiers of causal factors connected at each level by their logical relationships. In each tier, several factors that must all occur to create an outcome are coupled by logical AND, whereas several alternative factors, any one of which is sufficient to cause the outcome are connected by logical OR. Replacing the logical relationships with the relevant probabilistic equations allows us to calculate the aggregate probability of the scenario cumulatively from the probabilities of its causal factors.
But where’s the gain? Provided the factor tree is sufficiently exhaustive – that is, crucially, that we’ve understood the scenario and its causes well enough – the method massively reduces the uncertainties that render the results of frequentist assessment questionable. Quite apart from the weaknesses already mentioned, when using a frequentist scale we are obliged to slot events into typically quite broad categories of likelihood before any risk calculations are performed. This causes actual event likelihoods that fall somewhere between the defined category boundaries (in practice, almost all event likelihoods) to be variably misrepresented, leading to significant but subsequently undetectable assessment error. The probabilistic factor tree allows a much closer approximation to reality as likelihood values are determined by the relationships between the factors in the tree rather than being distorted by forcing them into a limited number of arbitrarily pre-defined categories.
So how do we make effective use of the probabilistic representation of likelihood? Merely assigning notional probabilities to scenarios against a quantised scale won’t get us any further than using frequentist assessment. But investigating causalities can hugely improve the quality of results. The first step is to build a ‘factor tree’ from our risk scenario. This consists of successive tiers of causal factors connected at each level by their logical relationships. In each tier, several factors that must all occur to create an outcome are coupled by logical AND, whereas several alternative factors, any one of which is sufficient to cause the outcome are connected by logical OR. Replacing the logical relationships with the relevant probabilistic equations allows us to calculate the aggregate probability of the scenario cumulatively from the probabilities of its causal factors.
But where’s the gain? Provided the factor tree is sufficiently exhaustive – that is, crucially, that we’ve understood the scenario and its causes well enough – the method massively reduces the uncertainties that render the results of frequentist assessment questionable. Quite apart from the weaknesses already mentioned, when using a frequentist scale we are obliged to slot events into typically quite broad categories of likelihood before any risk calculations are performed. This causes actual event likelihoods that fall somewhere between the defined category boundaries (in practice, almost all event likelihoods) to be variably misrepresented, leading to significant but subsequently undetectable assessment error. The probabilistic factor tree allows a much closer approximation to reality as likelihood values are determined by the relationships between the factors in the tree rather than being distorted by forcing them into a limited number of arbitrarily pre-defined categories.
REFERENCES
https://en.wikipedia.org/wiki/Law_of_large_numbers
https://en.wikipedia.org/wiki/Statistical_dispersion
https://www.gutenberg.org/files/15114/15114-pdf.pdf (particularly chapters 16 & 17)
https://www.britannica.com/topic/Boolean-algebra
https://www.sciencedirect.com/topics/engineering/quantisation
https://math.dartmouth.edu/~doyle/docs/huygens/huygens.pdf (English translation 1714)
https://en.wikipedia.org/wiki/Law_of_large_numbers
https://en.wikipedia.org/wiki/Statistical_dispersion
https://www.gutenberg.org/files/15114/15114-pdf.pdf (particularly chapters 16 & 17)
https://www.britannica.com/topic/Boolean-algebra
https://www.sciencedirect.com/topics/engineering/quantisation
https://math.dartmouth.edu/~doyle/docs/huygens/huygens.pdf (English translation 1714)
Mike Barwise
Director, BiR
02/10/2021